Ensiklopedia

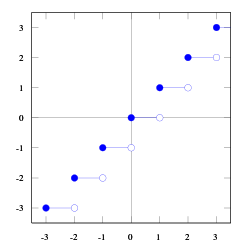
Dalam matematika , khususnya di bidang teori bilangan dan ilmu komputer , suatu fungsi ${\displaystyle f}$ dikatakan fungsi atap ( ceiling function ), dinotasikan oleh ${\displaystyle f(x)=\lceil x\rceil ={\text{ceil}}(x)}$ , adalah fungsi yang memetakan bilangan real ${\displaystyle x}$ ke bilangan bulat terkecil yang lebih besar daripada atau sama dengan ${\displaystyle x}$ . ^{[ 1 ]} Sebagai contoh, nilai dari ${\displaystyle \lceil 0,\!8\rceil =1}$ . Fungsi atap juga dapat disebut fungsi bilangan bulat terkecil ^{[ 2 ]} .

Sebaliknya, suatu fungsi ${\displaystyle f}$ dikatakan fungsi lantai ( floor function ), dinotasikan oleh ${\displaystyle f(x)=\lfloor x\rfloor ={\text{floor}}(x)}$ , adalah fungsi yang memetakan bilangan real ${\displaystyle x}$ ke bilangan bulat terbesar yang lebih kecil daripada atau sama dengan ${\displaystyle x}$ . ^{[ 1 ]} Sebagai contoh, nilai dari ${\displaystyle \lfloor 3,\!14\rfloor =3}$ . Fungsi lantai juga dapat disebut fungsi bilangan bulat terbesar . ^{[ 2 ]}

Galibnya, definisi pada fungsi bilangan bulat terbesar dan terkecil dapat ditulis sebagai

${\displaystyle \lfloor x\rfloor =\max\{n\in \mathbb {Z} \mid n\leq x\}}$ dan ${\displaystyle \lceil x\rceil =\min\{n\in \mathbb {Z} \mid n\geq x\}}$ . [ 1 ]

Hubungan kedua fungsi di atas dapat diterapkan pada salah satu fungsi berikut, yaitu bagian bilangan bulat ( bahasa Inggris : integer part ), di mana bilangan riil yang dipetakan ke fungsi tersebut sehingga menjadi bilangan bulat yang muncul sebelum bilangan desimal , dilambangkan ${\displaystyle [x]}$ atau terkadang dinotasikan sebagai ${\displaystyle \operatorname {int} (x)}$ ^{[ 3 ]} dan dirumuskan sebagai ^{[ 3 ] [ 4 ]}

${\displaystyle [x]={\begin{cases}\lfloor x\rfloor ,&{\text{jika }}x\geq 0\\\lceil x\rceil ,&{\text{jika }}x<0\end{cases}}}$ .

Untuk memahami lebih lanjut, tinjau ${\displaystyle \pi }$ yang bernilai ${\displaystyle 3.1415926\dots }$ , maka ${\displaystyle [\pi ]=3}$ . Hal yang serupa dengan bilangan bertandakan negatif, contohnya sederhananya, ${\textstyle \left[-{\frac {1}{2}}\right]=0}$ .

Fungsi atap dan lantai dikenal masuk dalam bagian bilangan bulat. ^{[ 5 ]} Namun, bagian bilangan bulat juga digunakan untuk pemotongan bilangan bulat mendekati 0 pada bilangan bulat negatif , yang berbeda dengan fungsi lantai di bilangan negatif.

Bagian bilangan bulat didefinisikan oleh Adrien-Marie Legendre pada tahun 1798. Selanjutnya, Carl Friedrich Gauss memperkenalkan penggunaan notasi tanda kurung kotak ^{[ 5 ]} untuk menuliskan fungsi bilangan bulat terbesar. Namun, tidak ada notasi standar untuk penulisan fungsi bilangan bulat terkecil. ^{[ 6 ]} Beberapa penulis bahkan menggunakan notasi ${\displaystyle ]x[}$ untuk penulisan fungsi bilangan bulat terkecil, yang tidak menjadi standar. ^{[ 6 ]}

Pada tahun 1962, memperkenalkan fungsi atap dan lantai dalam bukunya, . ^{[ 7 ]} Penggunaan notasi ini dipopulerkan oleh Donald Ervin Knuth ^{[ 8 ]} yang sekarang menjadi standar penggunaan dalam berbagai artikel teknis tanpa perlu penjelasan fungsi tersebut. ^{[ 6 ]}

Beberapa sifat yang terkandung dalam fungsi bilangan bulat besar dan fungsi bilangan bulat terkecil adalah sebagai berikut: ^{[ 9 ]}

• ${\displaystyle \lfloor x\rfloor \leq x\leq \lceil x\rceil }$ untuk suatu ${\displaystyle x}$ bilangan real .
• ${\displaystyle \lfloor x\rfloor =x}$ dan ${\displaystyle \lceil x\rceil =x}$ jika dan hanya jika ${\displaystyle x}$ adalah bilangan bulat.
• ${\displaystyle \lceil x\rceil -\lfloor x\rfloor =1}$ jika ${\displaystyle x}$ adalah bilangan real dan ${\displaystyle 0}$ bila ${\displaystyle x}$ bilangan bulat.
• Untuk suatu ${\displaystyle n}$ bilangan bulat, ${\displaystyle \lfloor x+n\rfloor =\lfloor x\rfloor +n}$ .

Untuk sifat fungsi bagian bilangan bulat, antara lain

• ${\displaystyle [-x]=-[x]}$

Beberapa penulis mendefinisikan bagian bulat sebagai fungsi bilangan bulat terbesar, menggunakan notasi berikut: ^{[ 10 ] [ 11 ] [ 12 ]}

• ${\displaystyle \lfloor x\rfloor =\lceil x\rceil =[x]}$ untuk ${\displaystyle x}$ adalah bilangan bulat.

Turunan fungsi bilangan bulat terbesar dan terkecil tidak terdiferensialkan bila ${\displaystyle x}$ adalah bilangan bulat. Bila ${\displaystyle x}$ bukanlah bilangan bulat, maka turunannya terdiferensialkan di mana-mana, ^{[ 13 ]} yakni bernilai 0.

Dalam integral , fungsi bilangan bulat terbesar dapat dinyatakan sebagai

• ${\displaystyle \int \lfloor x\rfloor \,\mathrm {d} x=x\lfloor x\rfloor }$ . ^{[ 14 ]}

Hal yang serupa dengan fungsi bilangan bulat terkecil,

• ${\displaystyle \int \lceil x\rceil \,\mathrm {d} x=x\lceil x\rceil }$ . ^{[ 15 ]}

Dalam representasi deret, fungsi bilangan bulat terbesar dirumuskan sebagai berikut:

• Dalam bentuk deret Fourier, dirumuskan

${\displaystyle \lfloor x\rfloor =x-{\frac {1}{2}}+{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}}$ asalkan ${\displaystyle x}$ bilangan real dan bukan bilangan bulat. ^{[ 16 ]}

Hal yang serupa dengan fungsi bilangan bulat terkecil.

• Dalam bentuk deret Fourier, dirumuskan

${\displaystyle \lceil x\rceil =x+{\frac {1}{2}}+{\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {\sin(2\pi kx)}{k}}}$ asalkan ${\displaystyle x}$ bilangan real dan bukan bilangan bulat. ^{[ 17 ]}

1. ^ ^{a b c} Sukardi, mathcyber1997.com: Materi, Soal, dan Pembahasan - Fungsi Lantai dan Fungsi Atap . Diakses pada 5 Agustus 2023.
2. ^ ^{a b} Gatot Muhsetyo (2019). Matematika Diskrit . Tanggerang Selatan: Universitas Terbuka. ISBN 9786023924127 . Diarsipkan dari versi asli tanggal 2023-06-02 . Diakses tanggal 2023-05-22 . Parameter |url-status= yang tidak diketahui akan diabaikan ( bantuan )
3. ^ ^{a b} Weisstein, Eric W. "Integer Part" . mathworld.wolfram.com (dalam bahasa Inggris). Diarsipkan dari versi asli tanggal 2023-06-23 . Diakses tanggal 2021-11-17 .
4. ^ "integer part" . planetmath.org . Diarsipkan dari versi asli tanggal 2021-05-06 . Diakses tanggal 2021-11-16 .
5. ^ ^{a b} "Floor and ceiling functions explained" . everything.explained.today . Diakses tanggal 2024-06-17 .
6. ^ ^{a b c} Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1994-02-28). Concrete Mathematics: A Foundation for Computer Science (dalam bahasa Inggris). Addison-Wesley Professional. hlm. 65. ISBN 978-0-13-438998-1 . Parameter |url-status= yang tidak diketahui akan diabaikan ( bantuan )
7. ^ Iverson, Kenneth E. (1962). A Programming Language (dalam bahasa Inggris). Wiley. hlm. 12. ISBN 978-0-471-43014-8 . Parameter |url-status= yang tidak diketahui akan diabaikan ( bantuan )
8. ^ "1.4: The Floor and Ceiling of a Real Number" . Mathematics LibreTexts (dalam bahasa Inggris). 2021-08-14 . Diakses tanggal 2024-06-17 .
9. ^ "Properties of Floors and Ceilings" . www.bookofproofs.org . Diarsipkan dari versi asli tanggal 2021-11-16 . Diakses tanggal 2021-11-16 .
10. ^ Luke Heaton, A Brief History of Mathematical Thought , 2015, ISBN 1472117158 (n.p.)
11. ^ Albert A. Blank et al. , Calculus: Differential Calculus , 1968, hlm. 259
12. ^ John W. Warris, Horst Stocker, Handbook of mathematics and computational science , 1998, ISBN 0387947469 , hlm. 151
13. ^ "Differentiable" . www.mathsisfun.com . Diarsipkan dari versi asli tanggal 2023-03-09 . Diakses tanggal 2021-11-24 .
14. ^ "Floor function: Integration (subsection 21/01/01)" . functions.wolfram.com . Diarsipkan dari versi asli tanggal 2019-09-13 . Diakses tanggal 2021-11-24 .
15. ^ "Ceiling function: Integration (subsection 21/01/01)" . functions.wolfram.com . Diarsipkan dari versi asli tanggal 2021-11-24 . Diakses tanggal 2021-11-24 .
16. ^ "Floor function: Series representations (subsection 06/01)" . functions.wolfram.com . Diarsipkan dari versi asli tanggal 2021-11-26 . Diakses tanggal 2021-11-26 .
17. ^ "Ceiling function: Series representations" . functions.wolfram.com . Diarsipkan dari versi asli tanggal 2021-11-24 . Diakses tanggal 2021-11-26 .