Ensiklopedia

Kubus
Kubus berbentuk .
Jenis	bangun ruang Platonik
Muka	6
	12
titik sudut	8
	V 3.3.3.3
	3
Simbol Schläfli	{4,3}
	O h , B 3 , [4,3], (* 432)
Sudut dihedral ( derajat )	90°
Sifat-sifat	beraturan, cembung zonohedron
Jaring

Dalam geometri , kubus adalah tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen berbentuk bujur sangkar. Kubus memiliki 6 sisi , 12 , dan 8 titik sudut . Kubus juga disebut dengan bidang enam beraturan . ^{[ 1 ]} Selain itu, kubus juga merupakan bentuk khusus dalam prisma segi empat , dan juga termasuk salah satu dari bangun ruang Platonik .

Kubus adalah bangun ruang yang terdiri atas enam buah sisi (atau muka ) bujur sangkar yang kongruen . Kubus memiliki 12 buah rusuk. Karena mukanya kongruen, kubus memiliki rusuk yang sama panjang. Selain itu, kubus memiliki delapan buah titik sudut dan memiliki diagonal ruang dengan panjang yang sama. ^{[ 1 ]}

pada kotak kue yang berbetuk kubus, apabila diiris pada rusuk-rusuk tertentu dan direbahkan pada bangun datar, maka bangun datar itu dinamakan jaring-jaring kubus. ^{[ 2 ]}

Diagonal bidang adalah garis yang menghubungkan dua sudut berlawanan pada suatu bidang datar persegi (pada kubus). Suatu kubus memiliki 12 diagonal bidang yang kongruen. ^{[ 2 ]}

Diagonal ruang adalah garis yang menghubungkan dua titik sudut yang tidak terletak pada satu bidang yang sama dalam sebuah bangun ruang. Diagonal ruang pada kubus ada 4 buah. ^{[ 2 ]}

Bidang diagonal adalah bidang yang terbentuk oleh dua diagonal bidang yang berpotongan atau dua sisi yang tidak sejajar dalam suatu bangun ruang. Bidang diagonal pada kubus ada sebanyak 6 buah. ^{[ 2 ]}

Sebuah kubus dengan panjang rusuk ${\displaystyle s}$ memiliki luas permukaan ^{[ 3 ]} $${\displaystyle L=6s^{2},}$$ yakni enam kali luas persegi.

Contoh :

Luas permukaan suatu kubus yang memiliki panjang rusuk 12 cm adalah $${\displaystyle L=6X12^{2},}$$ L = 6 X 12 X 12 $${\displaystyle L=384cm^{3}}$$

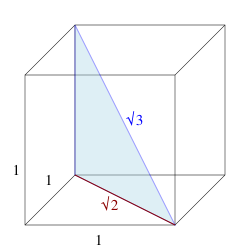
Diagonal bidang dari kubus ( ${\displaystyle d_{\text{bidang}}}$ ) beserta keseluruhannya ( ${\displaystyle d_{\text{seluruh sisi}}}$ ), dan diagonal ruang dari kubus ( ${\displaystyle d_{\text{ruang}}}$ ) beserta keseluruhannya ( ${\displaystyle d_{\text{seluruh ruang}}}$ ), juga masing-masing dirumuskan sebagai

${\displaystyle {\begin{aligned}d_{\text{bidang}}&=s{\sqrt {2}},\\d_{\text{seluruh bidang}}&=6s{\sqrt {2}},\\d_{\text{ruang}}&=s{\sqrt {3}},\\d_{\text{seluruh ruang}}&=4s{\sqrt {3}}.\end{aligned}}}$

Contoh :

hitunglah panjang diagonal bidang dan diagonal ruang dari kubus yang memiliki panjang sisi 7 cm !

jawab : $${\displaystyle s=7cm}$$ ${\displaystyle {\begin{aligned}d_{\text{bidang}}&=7{\sqrt {2}}cm,\\d_{\text{ruang}}&=7{\sqrt {3}}cm.\end{aligned}}}$

Luas beserta keseluruhannya, masing-masing dapat dirumuskan sebagai $${\displaystyle {\begin{aligned}L_{\text{bidang diagonal}}&=s^{2}{\sqrt {2}},\\L_{\text{seluruh bidang diagonal}}&=6s^{2}{\sqrt {2}}.\end{aligned}}}$$ Contoh :

luas bidang diagonal dari kubus yang memiliki panjang rusuk 7 cm adalah ... $${\displaystyle {\begin{aligned}s=7cm,\\L_{\text{bidang diagonal}}&=s^{2}{\sqrt {2}},\\L_{\text{bidang diagonal}}&=7^{2}{\sqrt {2}}=49{\sqrt {2}}cm^{2},\\L_{\text{seluruh bidang diagonal}}&=6s^{2}{\sqrt {2}},\\L_{\text{seluruh bidang diagonal}}&=6X7^{2}{\sqrt {2}}=294{\sqrt {2}}cm^{2}.\end{aligned}}}$$

Selain itu, kubus dengan panjang rusuk yang sama memiliki volume ^{[ 3 ]}

$${\displaystyle V=s^{3}}$$ contoh :

Ahmad mempunyai rubik, namun dengan ukuran lima satuan persegi. Dia ingin mengganti semua warna pada rubik tersebut dengan menempel stiker warna persegi. Bantu Ahmad untuk menentukan: ^{[ 4 ]}

• Banyak warna stiker yang dia butuhkan
• Banyak stiker yang dibutuhkan untuk setiap warna
• Banyak total stiker yang dibutuhkan

( doubling the cube ), atau disebut dengan masalah Delian, adalah masalah yang dicetuskan oleh . Masalah ini melibatkan konstruksi sebuah kubus dengan menggunakan , dan konstruksi tersebut dimulai dari panjang rusuk dari kubus dan mengonstruksi panjang rusuk kubus dengan dua kali lipatnya volume dari kubus sebelumnya. Sayangnya, masalah ini masih belum terpecahkan. Hingga pada tahun 1837, membuktikan bahwa konstruksi tersebut mustahil sebab akar pangkat tiga dari 2 bukanlah ( constructible number ).

• Weisstein, Eric W. "Cube" . MathWorld .
• Cube: Interactive Polyhedron Model
• Volume kubus , dengan animasi interaktif
• Cube (Situs Robert Webb)